合同二等辺化線点

幾何学において、合同二等辺化線点（ごうどうにとうへんかせんてん、英:congruent isoscelizers point）は、三角形の中心の一つである。 Encyclopedia of Triangle Centersでは X(173)として登録されている。1989年、ピーター・イフ の三角形幾何学の研究で発見された。

定義

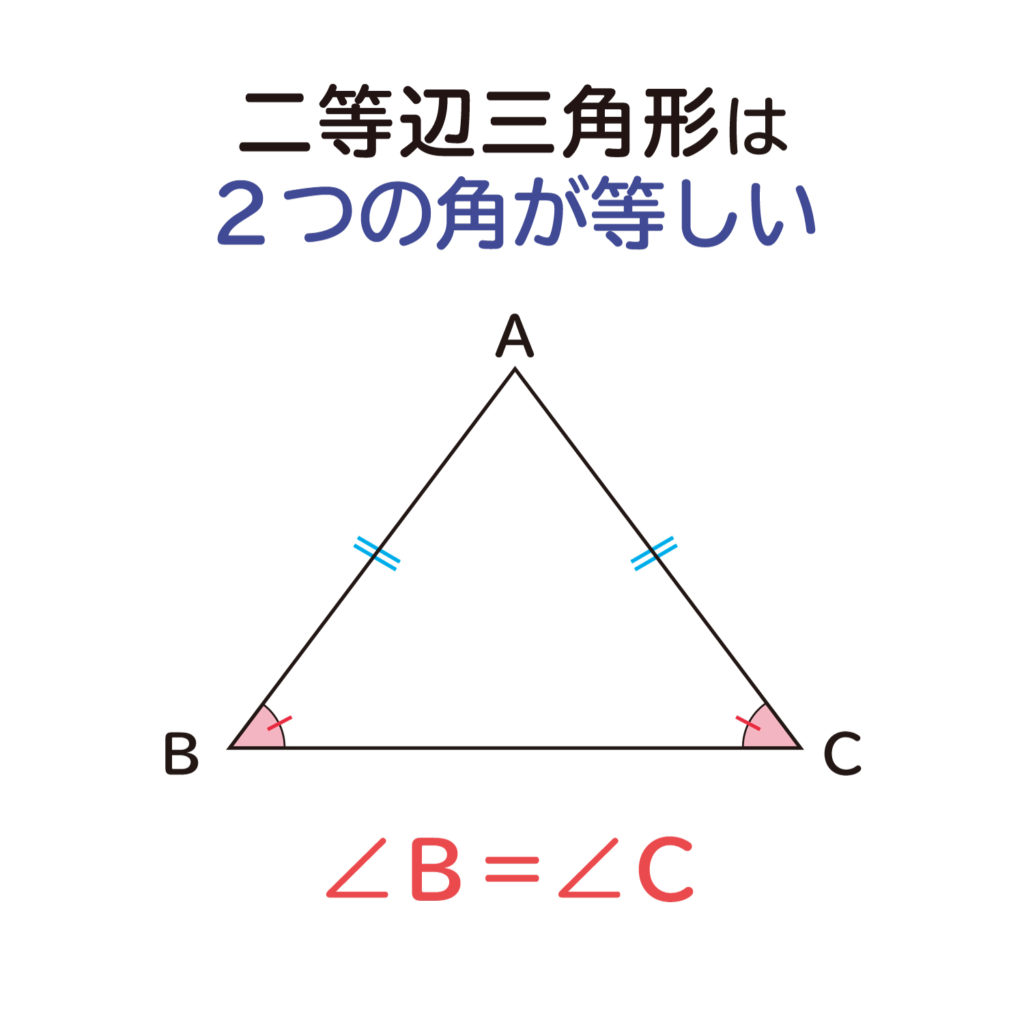
△ABCについて、△AP₁Q₁が二等辺三角形となるような線P₁Q₁をAの二等辺化線（ isoscelizer）という。ただし、P₁,Q₁はそれぞれAB,AC上にあるとする。また二等辺化線は角の二等分線の垂線である。

△ABCについて、A, B, Cの二等辺化線をそれぞれ P₁Q₁, P₂Q₂, P₃Q₃とする。このとき線分P₁Q₁, P₂Q₂, P₃Q₃が同じ長さかつP₁Q₁, P₂Q₂, P₃Q₃が一点で交わるようにすることができる。この点を合同二等辺化線点という。

性質

• △ABCの合同二等辺化線点の三線座標は以下の式で与えられる。

$${\displaystyle {\begin{array}{ccccc}\cos {\frac {B}{2}} \cos {\frac {C}{2}}-\cos {\frac {A}{2}}&:&\cos {\frac {C}{2}} \cos {\frac {A}{2}}-\cos {\frac {B}{2}}&:&\cos {\frac {A}{2}} \cos {\frac {B}{2}}-\cos {\frac {C}{2}}\\[4pt]=\quad \tan {\frac {A}{2}} \sec {\frac {A}{2}}\quad \ \ &:&\tan {\frac {B}{2}} \sec {\frac {B}{2}}&:&\tan {\frac {C}{2}} \sec {\frac {C}{2}}\end{array}}}$$

• 接触三角形の接触三角形と元の三角形の配景の中心は合同二等辺化線点である。 この事実は合同二等辺化線点の作図から示すことができる。
• Yff Central tringleと傍心三角形のクローソン点である。

等角共役点

合同二等辺化線点の等角共役点は合同内接円二等辺化線点（Congurent incircles isocelizers point）である。定義は次の通り。

△ABCについて、点Pを通る、それぞれA, B, Cの二等辺化線と2辺が成す三角形の内接円がすべて合同であるような点Pを合同内接円二等辺化線点という。

合同内接円二等辺化線点は、内心と傍心三角形の内心と共線である。

Encyclopedia of Triangle CentersではX(258)で紹介されており、三線座標は次の式で与えられる。

${\displaystyle \tan({\frac {A}{2}})-\sec({\frac {A}{2}}):\tan({\frac {B}{2}})-\sec({\frac {B}{2}}):\tan({\frac {C}{2}})-\sec({\frac {C}{2}})}$

関連

• イフ合同心
• 合同辺平行線点

出典