ツェラーの公式

ツェラーの公式（ツェラーのこうしき、英: Zeller's congruence、独: Zellers Kongruenz）とは西暦（グレゴリオ暦またはユリウス暦）の年・月・日から、その日の曜日を算出する公式である。ドイツの数学者であるクリスティアン・ツェラー (Christian Zeller) が1882年に考案した。

特定の日からの通算日数（ユリウス通日やRata Dieなど）を求め、その剰余から曜日を求める計算と本質は同じである。

呼称および表記

Zeller's congruence は直訳すると「Zeller の合同式」といった意味になるが、日本では主に「Zeller の公式」と呼ばれる。またカタカナ表記はドイツ語読みで「ツェラーの公式」と記すのが一般的だが、英語読みで「ゼラーの公式」と表記されることもある。

公式

y 年 m 月 d 日の曜日を求める。

ただし、1月と2月は、前年のそれぞれ13月・14月として扱う。たとえば、2025年1月1日・2月1日は、2024年13月1日・14月1日とする。また、紀元前 ${\displaystyle {\hat {y}}}$ 年は西暦 ${\displaystyle 1-{\hat {y}}}$ 年として扱う（天文学的紀年法）。たとえば、紀元前1年・前2年・前3年は、0年・－1年・－2年となる。

曜日 h は次の式で求められる（ h は、0 から 6 でそれぞれ土曜日から金曜日を表す）：

${\displaystyle h=\left(d \left\lfloor {\frac {26(m 1)}{10}}\right\rfloor Y \left\lfloor {\frac {Y}{4}}\right\rfloor {\mathit {\Gamma }}\right){\bmod {7}}}$

${\displaystyle {\mathit {\Gamma }}}$ はグレゴリオ暦 (Gregorian) かユリウス暦 (Julian) かで変わる項で、

${\displaystyle {\mathit {\Gamma }}={\begin{cases}-2C \left\lfloor {\frac {C}{4}}\right\rfloor &{\mbox{: Gregorian }}(1582\lessapprox y)\\-C 5&{\mbox{: Julian }}(4\lessapprox y\lessapprox 1582)\end{cases}}}$

ただし

${\displaystyle C=\left\lfloor {\frac {y}{100}}\right\rfloor }$

${\displaystyle Y=y{\bmod {1}}00}$

とする。

${\displaystyle \lfloor x\rfloor }$は x を超えない（x以下）の最大の整数（床関数）であり、x mod n は x を n で割った剰余である。C と Y は、（西暦が4桁の場合）西暦の上2桁と下2桁を表す中間変数で、たとえば2025年なら、それぞれ20と25になる。

適用範囲

以上の2つの計算式は、それぞれの暦法を過去または未来に単純に延長して使うのであれば、年数の有効範囲の限界はない（先発グレゴリオ暦、先発ユリウス暦を参照）。

しかし歴史上の実際の年月日についての曜日を知るには注意が必要である。

グレゴリウス13世は、ユリウス暦の1582年10月4日木曜日の翌日を、グレゴリオ暦の10月15日金曜日として実施した。

しかし、各国・各地方が実際にグレゴリオ暦を導入した時期は異なる場合がある。例えばイギリス帝国ではユリウス暦の1752年9月2日水曜日の翌日をグレゴリオ暦の9月14日木曜日として導入している。

そのため、知りたい年月日がユリウス暦なのかグレゴリオ暦なのかによって使用すべき式を選ぶ必要がある。

また、ガイウス・ユリウス・カエサルがユリウス暦を制定・実施したのは紀元前45年1年1月であるが、その直後の紀元前44年にカエサルが暗殺されたため、その後の閏年の設定が誤っていた時期と、それを補正した期間があった。これらの時期の閏年が何年に実施されたかについては、さまざまな主張があり議論になっている。少なくとも西暦8年以降は本来のユリウス暦のルールに則って閏年が実施されているとされている。

ゆえに西暦8年以前の日付の実際の曜日を求めるのは困難である。

ISO 8601 との関係

日付の表記の国際規格である ISO 8601が定める D（1 から 7 でそれぞれ月曜日から日曜日）を求めるには、次の式

${\displaystyle D=\left(\left(d \left\lfloor {\frac {26(m 1)}{10}}\right\rfloor Y \left\lfloor {\frac {Y}{4}}\right\rfloor {\mathit {\Gamma }} 5\right){\bmod {7}}\right) 1}$

を使う。

コンピュータでの計算

ツェラーの公式では年を2つの中間変数を使って計算しているがこれは筆算での計算の容易化のためで、コンピュータで計算する場合には中間変数を用いない式に変形して使用することがある。

変形したグレゴリオ暦の式の例は以下の通り（1月、2月を前年の13月、14月として扱うのは同様）。

${\displaystyle h'=\left(y \left\lfloor {\frac {y}{4}}\right\rfloor -\left\lfloor {\frac {y}{100}}\right\rfloor \left\lfloor {\frac {y}{400}}\right\rfloor \left\lfloor {\frac {13m 8}{5}}\right\rfloor d\right){\bmod {7}}}$

同様に変形したユリウス暦の式の例は以下の通り。

${\displaystyle h'=\left(y \left\lfloor {\frac {y}{4}}\right\rfloor \left\lfloor {\frac {13m 8}{5}}\right\rfloor d 5\right){\bmod {7}}}$

この場合の曜日 h' は、0 から 6 でそれぞれ日曜日から土曜日を表す。

実装するうえでは、いくつか注意すべき点がある。

• 負数の剰余は、開発言語などによって異なる動作をすることがある（剰余演算を参照）。上記の式は数学的定義の通り、例えば -1 mod 7 = 6 であることが前提である。
• 負数の整数除算の丸めは、開発言語などによって異なる動作をすることがある（端数処理を参照）。整数除算を使って床関数と同じ結果を得るには、負の無限大への丸めである必要がある。上記の式を整数除算でそのまま記述するには、例えば -10 / 4 が -3 である必要がある。
• 開発言語やライブラリなどによっては、例えば1月を 0 とあらわすことがあるため、必要であれば変換を行う。

以下に Python3 でのグレゴリオ暦版の実装例を示す（以下の関数では月を 1 - 12 の値で受け取り、関数内に1月、2月を前年の13月、14月として扱うための処理を含む）。

同様の条件で、C言語での実装例を示す。

ただし、負数の年を考慮しなくてよい場合、つまり西暦0年（紀元前1年）3月1日以降のみを対象とすればよい場合には、C言語でもPython3と同様のシンプルな実装で問題ない。

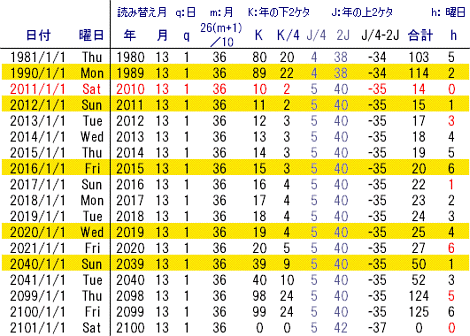
計算例

グレゴリオ暦での曜日の計算例を示す。

ユリウス暦での曜日の計算例を示す。

ツェラーの公式の導出

曜日は７日間で循環しているので、上記【※】式の 7 の剰余を求めることで曜日が判明する。即ち、

である。

このとき h' のとり得る値は 0 から 6 で、それぞれ日曜日から土曜日を表す。

（現行のグレゴリオ暦は、1582年10月15日にこの日を金曜日であるとして施行されたが、この日を起点に遡ってグレゴリオ暦を適用すると1年1月1日は月曜日となるため h' の値が表す曜日がこのような並びになる）

【I】式が 7 の剰余である事を利用すると、以下の通り変形できる。

${\displaystyle {\begin{array}{lcl}h'&=&\left(7(52y-62) y \left\lfloor {\frac {y}{4}}\right\rfloor -\left\lfloor {\frac {y}{100}}\right\rfloor \left\lfloor {\frac {y}{400}}\right\rfloor \left\lfloor {\frac {153(m 1)}{5}}\right\rfloor 6 d\right){\bmod {7}}\\&=&\left(y \left\lfloor {\frac {y}{4}}\right\rfloor -\left\lfloor {\frac {y}{100}}\right\rfloor \left\lfloor {\frac {y}{400}}\right\rfloor \left\lfloor {\frac {153(m 1)}{5}}\right\rfloor 6 d\right){\bmod {7}}\end{array}}}$

ここで、床関数の性質（ ${\displaystyle \lfloor a\rfloor b=\lfloor a b\rfloor }$ , ただし b は整数）を利用すると、

${\displaystyle {\begin{array}{lcl}h'&=&\left(y \left\lfloor {\frac {y}{4}}\right\rfloor -\left\lfloor {\frac {y}{100}}\right\rfloor \left\lfloor {\frac {y}{400}}\right\rfloor \left\lfloor {\frac {153(m 1)}{5}} 6\right\rfloor d\right){\bmod {7}}\\&=&\left(y \left\lfloor {\frac {y}{4}}\right\rfloor -\left\lfloor {\frac {y}{100}}\right\rfloor \left\lfloor {\frac {y}{400}}\right\rfloor \left\lfloor {\frac {153m 153 30}{5}}\right\rfloor d\right){\bmod {7}}\\&=&\left(y \left\lfloor {\frac {y}{4}}\right\rfloor -\left\lfloor {\frac {y}{100}}\right\rfloor \left\lfloor {\frac {y}{400}}\right\rfloor \left\lfloor {\frac {153m 183}{5}}\right\rfloor d\right){\bmod {7}}\\&=&\left(y \left\lfloor {\frac {y}{4}}\right\rfloor -\left\lfloor {\frac {y}{100}}\right\rfloor \left\lfloor {\frac {y}{400}}\right\rfloor \left\lfloor {\frac {35(4m 5) 13m 8}{5}}\right\rfloor d\right){\bmod {7}}\\&=&\left(y \left\lfloor {\frac {y}{4}}\right\rfloor -\left\lfloor {\frac {y}{100}}\right\rfloor \left\lfloor {\frac {y}{400}}\right\rfloor \left\lfloor 7(4m 5) {\frac {13m 8}{5}}\right\rfloor d\right){\bmod {7}}\end{array}}}$

さらに、h' が 7 の剰余であることを利用して、

${\displaystyle h'=\left(y \left\lfloor {\frac {y}{4}}\right\rfloor -\left\lfloor {\frac {y}{100}}\right\rfloor \left\lfloor {\frac {y}{400}}\right\rfloor \left\lfloor {\frac {13m 8}{5}}\right\rfloor d\right){\bmod {7}}}$

と変形できる。

y = 100C Y ( 0 ≦ Y ≦ 99, C, Y は整数)と置くと、以下の通り変形される。

${\displaystyle {\begin{array}{lcl}h'&=&\left(100C Y \left\lfloor {\frac {100C Y}{4}}\right\rfloor -\left\lfloor {\frac {100C Y}{100}}\right\rfloor \left\lfloor {\frac {100C Y}{400}}\right\rfloor \left\lfloor {\frac {13m 8}{5}}\right\rfloor d\right){\bmod {7}}\\&=&\left(100C Y \left\lfloor 25C {\frac {Y}{4}}\right\rfloor -\left\lfloor C {\frac {Y}{100}}\right\rfloor \left\lfloor {\frac {C}{4}} {\frac {Y}{400}}\right\rfloor \left\lfloor {\frac {26m 26}{10}}-1\right\rfloor d\right){\bmod {7}}\\&=&\left(100C Y \left\lfloor 25C {\frac {Y}{4}}\right\rfloor -\left\lfloor C {\frac {Y}{100}}\right\rfloor \left\lfloor {\frac {C}{4}} {\frac {Y}{400}}\right\rfloor \left\lfloor {\frac {26m 26}{10}}\right\rfloor -1 d\right){\bmod {7}}\\&=&\left(100C Y 25C \left\lfloor {\frac {Y}{4}}\right\rfloor -C-\left\lfloor {\frac {Y}{100}}\right\rfloor \left\lfloor {\frac {C}{4}} {\frac {Y}{400}}\right\rfloor \left\lfloor {\frac {26m 26}{10}}\right\rfloor d-1\right){\bmod {7}}\\&=&\left(124C Y \left\lfloor {\frac {Y}{4}}\right\rfloor -\left\lfloor {\frac {Y}{100}}\right\rfloor \left\lfloor {\frac {C}{4}} {\frac {Y}{400}}\right\rfloor \left\lfloor {\frac {26m 26}{10}}\right\rfloor d-1\right){\bmod {7}}\\&=&\left(\left(7\times 18\right)C-2C Y \left\lfloor {\frac {Y}{4}}\right\rfloor -\left\lfloor {\frac {Y}{100}}\right\rfloor \left\lfloor {\frac {C}{4}} {\frac {Y}{400}}\right\rfloor \left\lfloor {\frac {26m 26}{10}}\right\rfloor d-1\right){\bmod {7}}\end{array}}}$

h' が 7 の剰余であることを利用して、

${\displaystyle h'=\left(-2C Y \left\lfloor {\frac {Y}{4}}\right\rfloor -\left\lfloor {\frac {Y}{100}}\right\rfloor \left\lfloor {\frac {C}{4}} {\frac {Y}{400}}\right\rfloor \left\lfloor {\frac {26m 26}{10}}\right\rfloor d-1\right){\bmod {7}}}$

ここで 0 ≦ Y ≦ 99より、0 ≦ Y/100 ≦ 0.99 であり、

${\displaystyle \left\lfloor {\frac {Y}{100}}\right\rfloor =0}$

同様に 0 ≦ Y/400 ≦ 0.2475 であり、また C/4 の小数部分は、0, 0.25, 0.5, 0.75 の何れかの値を取る為、C/4 Y/400 の小数部分は高々 0.75 0.2475 = 0.9975 であり、

${\displaystyle \left\lfloor {\frac {C}{4}} {\frac {Y}{400}}\right\rfloor =\left\lfloor {\frac {C}{4}}\right\rfloor }$

としてよい。よって、

${\displaystyle h'=\left(-2C Y \left\lfloor {\frac {Y}{4}}\right\rfloor \left\lfloor {\frac {C}{4}}\right\rfloor \left\lfloor {\frac {26m 26}{10}}\right\rfloor d-1\right){\bmod {7}}}$

このとき h' のとり得る値は 0 から 6 で、それぞれ日曜日から土曜日を表す（【I】式の場合と同様）。

演算（項）数を減らすためこの式の被除数に 1 加算すると

${\displaystyle h=\left(-2C Y \left\lfloor {\frac {Y}{4}}\right\rfloor \left\lfloor {\frac {C}{4}}\right\rfloor \left\lfloor {\frac {26(m 1)}{10}}\right\rfloor d\right){\bmod {7}}}$

となり、ツェラーの公式が導出できる。

このとき h のとり得る値は 0 から 6 で、それぞれ土曜日から金曜日を表す（被除数に 1 加算しているため【I】式の場合と比べ、１日分のずれが生じた）。

日本での紹介

ツェラーの公式が日本で最初に紹介された時期は不明だが、以下の事例がある。

1921年（大正10年）の『日本中等教育数学会雑誌』にツェラーの公式が紹介されている。

ただし「ツェラーの公式を紹介している記事」を紹介しており、Zellerの名前は記載されていない。そのため、ツェラーの公式を Philip Franklin が1921年に考案したと間違えられることもある。

1938年（昭和13年）に『月刊数学』でZellerの名前で紹介されている。

どちらの事例でもグレゴリオ暦版の公式だけが紹介されている。

脚注

注釈

出典

外部リンク

• ドイツ語版ウィキソースに本記事に関連した原文があります："Kalender-Formeln" 1886/1887
• Mainly on Zeller's algorithms at the Wayback Machine (archived 20140111)
• RFC 3339 - 付録Bに、ツェラーの公式の変形（中間変数は使うが、日曜日は0になるように）したものが記載されている。