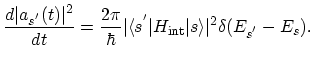尤度方程式

尤度方程式（ゆうどほうていしき、英: likelihood equation）とは、統計学において、対数尤度関数の極値条件を与える方程式の事。統計的推定法の一つである最尤法において、尤度関数を最大化する最尤推定値を求める際に用いられる。

概要

独立同分布を満たす ${\displaystyle n}$ 個の確率変数 ${\displaystyle {\boldsymbol {D}}=\{D_{i}\mid i\in \{1,..,n\}\}}$ とその観測値 ${\displaystyle {\boldsymbol {d}}=\{d_{i}\mid i\in \{1,..,n\}\}}$ を定義する。すなわち真の分布から ${\displaystyle n}$ 個の観測値（データ）が無作為抽出された状況を考える。

ここで確率密度関数 ${\displaystyle f(X|{\boldsymbol {\theta }})}$ に従う確率モデルを導入する。ここで ${\displaystyle {\boldsymbol {\theta }}={(\theta _{1},..,\theta _{p})}}$ は分布パラメータ群であり、パラメータ空間Θ ⊂ R^pに値を持つ。この確率モデルが ${\displaystyle {\boldsymbol {d}}}$ を最も良く説明する ${\displaystyle {\boldsymbol {\theta }}}$ を求めたい。ゆえに最尤推定をおこなう。

このとき独立同分布条件により、尤度関数 ${\displaystyle L({\boldsymbol {\theta }}|{\boldsymbol {d}})}$ と対数尤度関数 ${\displaystyle l({\boldsymbol {\theta }}|{\boldsymbol {d}})}$ は以下で定義される。

${\displaystyle L({\boldsymbol {\theta }}|{\boldsymbol {d}})=\prod _{i=1}^{n}f(X=d_{i}|{\boldsymbol {\theta }})}$

${\displaystyle l({\boldsymbol {\theta }}|{\boldsymbol {d}})=\ln {L({\boldsymbol {\theta }}|{\boldsymbol {d}})}=\sum _{i=1}^{n}\ln {f(X=d_{i}|{\boldsymbol {\theta }})}}$

すなわちあるデータ群に対するモデルの尤度関数は、各観測値に対する尤度関数の積（対数尤度の場合は和）となる。

最尤法では対数尤度関数を最大化する ${\displaystyle {\boldsymbol {\theta }}}$ が最尤推定値 ${\displaystyle {\hat {\boldsymbol {\theta }}}}$ として定まる。このとき ${\displaystyle {\hat {\boldsymbol {\theta }}}}$ は次の極値条件を満たす。

${\displaystyle {\frac {\partial }{\partial {\boldsymbol {\theta }}}}l({\boldsymbol {\theta }}|{\boldsymbol {d}})=\mathbf {0} }$

この方程式を尤度方程式という。左辺の勾配ベクトル：

${\displaystyle \mathbf {S} ({\boldsymbol {d}},{\boldsymbol {\theta }}):={\frac {\partial }{\partial {\boldsymbol {\theta }}}}l({\boldsymbol {\theta }}|{\boldsymbol {d}})}$

は、スコア関数、もしくは単にスコアと呼ばれる。多くの場合、最尤推定値の推定は、尤度方程式を解く問題、すなわち、スコアをゼロとするパラメータθ∈ Θを求める問題に帰着する。

例

正規分布

X_i (i=1,..,n)が平均をμ、分散をσ²とする正規分布に従うとする（X ∼ N(μ, σ²)）。このとき、対数尤度関数は

${\displaystyle l(\mu ,\sigma ^{2},\mathbf {x} )=-{\frac {n}{2}}\ln {2\pi }-{\frac {n}{2}}\ln {\sigma ^{2}}-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}}$

であり、尤度方程式は

${\displaystyle {\frac {\partial l(\mu ,\sigma ^{2},\mathbf {x} )}{\partial \mu }}={\frac {1}{\sigma ^{2}}}\sum _{i=1}^{n}(x_{i}-\mu )=0}$

${\displaystyle {\frac {\partial l(\mu ,\sigma ^{2},\mathbf {x} )}{\partial \sigma ^{2}}}=-{\frac {n}{2\sigma ^{2}}} {\frac {1}{2(\sigma ^{2})^{2}}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}=0}$

となる。これらを整理すると最尤推定値として

${\displaystyle {\hat {\mu }}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$

${\displaystyle {\hat {\sigma ^{2}}}={\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}}$

を得る。

ワイブル分布

X_i (i=1,..,n)が形状パラメータをβ、尺度パラメータをηとするワイブル分布に従うとする。このとき、対数尤度関数は

${\displaystyle l(\eta ,\beta ,\mathbf {x} )=n\ln {\beta }-n\beta \ln {\eta } (\beta -1)\sum _{i=1}^{n}\ln {x_{i}}-{\frac {1}{\eta ^{\beta }}}\sum _{i=1}^{n}x_{i}^{\beta }}$

であり、尤度方程式は

${\displaystyle {\frac {\partial l(\eta ,\beta ,\mathbf {x} )}{\partial \eta }}=-{\frac {n\beta }{\eta }}-{\frac {\beta }{\eta ^{(\beta 1)}}}\sum _{i=1}^{n}x_{i}^{\beta }=0}$

${\displaystyle {\frac {\partial l(\eta ,\beta ,\mathbf {x} )}{\partial \beta }}={\frac {n}{\beta }}-n\ln {\eta } \sum _{i=1}^{n}\ln {x_{i}} {\frac {\ln {\eta }}{\eta ^{\beta }}}\sum _{i=1}^{n}x_{i}^{\beta } {\frac {1}{\eta ^{\beta }}}\sum _{i=1}^{n}\ln {x_{i}}x_{i}^{\beta }=0}$

となる。 これらを整理すると最尤推定値ˆη、ˆβが満たすべき関係式

${\displaystyle {\hat {\eta }}=\left({\frac {1}{n}}\sum _{i=1}^{n}x_{i}^{\hat {\beta }}\right)^{\frac {1}{\hat {\beta }}}}$

${\displaystyle {\frac {1}{\hat {\beta }}} {\frac {1}{n}}\sum _{i=1}^{n}\ln {x_{i}}-{\frac {\sum _{i=1}^{n}x_{i}^{\hat {\beta }}\ln {x_{i}}}{\sum _{i=1}^{n}x_{i}^{\hat {\beta }}}}=0}$

を得る。第二式を満たすˆβを数値的に求めれば、第一式よりˆηも定まる。

ガンマ分布

X_i (i=1,..,n)が形状パラメータをα、尺度パラメータをβとするガンマ分布に従うとする（X ∼ Γ(α, β)）。このとき、対数尤度関数は

${\displaystyle l(\alpha ,\beta ,\mathbf {x} )=-n\ln {\Gamma (\alpha )}-n\alpha \ln {\beta } (\alpha -1)\sum _{i=1}^{n}\ln {x_{i}}-{\frac {1}{\beta }}\sum _{i=1}^{n}x_{i}}$

であり、尤度方程式は

${\displaystyle {\frac {\partial l(\alpha ,\beta ,\mathbf {x} )}{\partial \alpha }}=-n\psi (\alpha )-n\ln {\beta } (\alpha -1)\sum _{i=1}^{n}\ln {x_{i}}=0}$

${\displaystyle {\frac {\partial l(\alpha ,\beta ,\mathbf {x} )}{\partial \beta }}=-{\frac {n\alpha }{\beta }} {\frac {1}{\beta ^{2}}}\sum _{i=1}^{n}x_{i}=0}$

となる。 ここではψ(α)はガンマ関数の対数微分であるディガンマ関数を表す。これらを整理すると最尤推定値ˆβ、ˆαが満たすべき関係式

${\displaystyle {\hat {\beta }}={\frac {1}{\hat {\alpha }}}{\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$

${\displaystyle {\hat {\alpha }}={\frac {{\frac {1}{n}}\sum _{i=1}^{n}x_{i}}{\left(\prod _{i=1}^{n}x_{i}\right)^{\frac {1}{n}}}}\exp {(\psi ({\hat {\alpha }}))}}$

を得る。第二式を満たすˆαを数値的に求めれば、第一式よりˆβも定まる。

数値解法

尤度方程式が解析的に解けない場合、S(θ*)=0を満たすθ*∈ Θを数値的に求めることが必要となる。

ニュートン＝ラフソン法

ニュートン＝ラフソン法では、反復計算により、最適解θ*を求める。反復計算のkステップ目で求まったパラメータをθ^(k)とする。スコア関数はテイラー展開により、

${\displaystyle \mathbf {S} (\mathbf {x} ,{\boldsymbol {\theta }})\simeq \mathbf {S} (\mathbf {x} ,{\boldsymbol {\theta }}^{(k)})-I({\boldsymbol {\theta }}^{(k)})({\boldsymbol {\theta }}-{\boldsymbol {\theta }}^{(k)})}$

と一次近似できる。ここでI(θ)は、

${\displaystyle I({\boldsymbol {\theta }})=-{\frac {\partial ^{2}}{\partial {\boldsymbol {\theta }}\partial {\boldsymbol {\theta }}^{T}}}\ln {L({\boldsymbol {\theta }},\mathbf {x} )}}$

で与えられる、対数尤度関数のヘッセ行列の符号を変えた行列である。ニュートン＝ラフソン法では、左辺をゼロとおくことで、θ^{(k 1)}を与える更新式

${\displaystyle {\boldsymbol {\theta }}^{(k 1)}={\boldsymbol {\theta }}^{(k)} I({\boldsymbol {\theta }}^{(k)})^{-1}\mathbf {S} (\mathbf {x} ,{\boldsymbol {\theta }}^{(k)})}$

を定める。

ニュートン＝ラフソン法は、最適解θ*の近傍で二次収束するため、収束が早い。すなわち、θ*の十分近くの適切な初期値を与えれば、

${\displaystyle ||{\boldsymbol {\theta }}^{(k)}-{\boldsymbol {\theta }}^{\ast }||\leq K||{\boldsymbol {\theta }}^{(k)}-{\boldsymbol {\theta }}^{\ast }||^{2}}$

を満たす正の定数Kが存在する。

一方で、ニュートン＝ラフソン法は各ステップで、対数尤度関数のヘッセ行列から定まるI(θ)の逆行列を計算する、もしくは、p次の連立方程式を解くことが必要となる。これらの計算量はO(p³)のオーダーであり、パラメータ数pが増えると、計算負荷が急激に増える。また、初期値の設定によっては、I(θ)は正定値とはならず、最適解θ*に収束しない場合がある。

フィッシャーのスコア法

ニュートン＝ラフソン法においては、各ステップで負の対数尤度関数の二階微分であるI(θ)を計算する必要がある。このI(θ)を求める計算は、場合によっては煩雑となる。分布によっては、I(θ)の期待値であるフィッシャー情報行列

${\displaystyle J({\boldsymbol {\theta }})=E_{\boldsymbol {\theta }}\left[-{\frac {\partial ^{2}}{\partial {\boldsymbol {\theta }}\partial {\boldsymbol {\theta }}^{T}}}\ln {L({\boldsymbol {\theta }},\mathbf {x} )}\right]=E_{\boldsymbol {\theta }}\left[{\frac {\partial }{\partial {\boldsymbol {\theta }}}}\ln {L({\boldsymbol {\theta }},\mathbf {x} }){\frac {\partial }{\partial {\boldsymbol {\theta }}^{T}}}\ln {L({\boldsymbol {\theta }},\mathbf {x} )}\right]}$

が、より簡潔に求まるため、I(θ)をJ(θ)で代用し、反復計算を

${\displaystyle {\boldsymbol {\theta }}^{(k 1)}={\boldsymbol {\theta }}^{(k)} J({\boldsymbol {\theta }}^{(k)})^{-1}\mathbf {S} (\mathbf {x} ,{\boldsymbol {\theta }}^{(k)})}$

とする。この方法をフィッシャーのスコア法と呼ぶ。

フィッシャー情報行列は非負定値であるため、ニュートン＝ラフソン法でのI(θ)の正定値性の問題を回避することができる。

脚注

参考文献

• Epps, T. W. (2013). Probability and Statistical Theory for Applied Researchers. World Scientific Pub Co Inc. ISBN 978-9814513159 
• Lehmann, E. L. (1983). Theory of Point Estimation. John Wiley & Sons Inc. ISBN 978-0471058496 
• Monahan, John F. (2011). Numerical Methods of Statistics. Cambridge Series in Statistical and Probabilistic Mathematics (2nd ed.). Cambridge University Press. ISBN 978-0521139519 

関連項目

• 最尤法