数理最適化

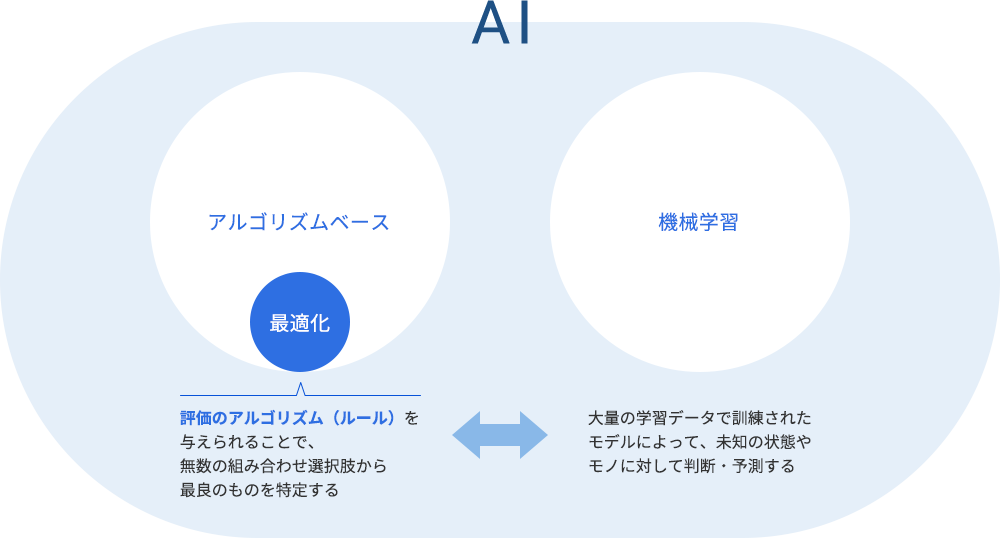
数学の計算機科学やオペレーションズリサーチの分野における数理最適化（すうりさいてきか、英: mathematical optimization）または数理計画法（英: mathematical programming）とは、（ある条件に関して）最もよい元を、利用可能な集合から選択することをいう。

最も簡単な最適化問題には、ある許された集合から入力をシステマティックに選び、函数の値を計算することによる実数函数の最大化と最小化がある。最適化理論とその手法の、他の形式への一般化は応用数学の広範な分野をなすものである。より一般に、最適化はある与えられた定義域（あるいは制約の集合）についてある目的函数の「利用可能な最も良い」値を見つけることも含む。そのような目的函数と定義域は多様な異なるタイプのものも含む。

最適化問題

最適化問題は、次のように表現される：

与えられるもの：ある集合 A から実数への函数 f : A ${\displaystyle \to }$ R

目的：A 内のすべての x に対して最小化問題であれば f(x₀) ≤ f(x) を満たす A 内の元 x₀（最小点）と、あるいは最大化問題であれば f(x₀) ≥ f(x) を満たす A 内の元 x₀（最大点）を見つけること。

このような問題は最適化問題（optimization）あるいは数理計画問題（mathematical programming）（コンピュータプログラミングとは直接的には関係ないが、例えば線型計画法では用いられる）と呼ばれる。多くの実世界での問題や理論的問題は、一般的な枠組みでモデル化される。物理学やコンピュータビジョンの分野における、この手法による問題は、エネルギー最小化（energy minimization）と呼ばれることもある。この場合、函数 f の値はモデル化されるシステムのエネルギーを表す。

典型的に集合 A はユークリッド空間 Rⁿ の部分集合であり、しばしばある制約の集合によって特徴づけられ、A の元は求められる等式あるいは不等式を満たす必要がある。f の定義域 A は探索空間（search space）あるいは選択集合（choice set）あるいは実行可能領域と呼ばれ、A の元は可能解（candidate solution, feasible solution）あるいは実行可能解と呼ばれる。

函数 f は、目的函数（objective function）や損失函数（loss function）、費用函数（cost function）、効用函数（utility function）、適合函数（fitness function）、エネルギー函数（energy function）あるいはエネルギー汎函数（energy functional）と呼ばれる。目的函数を最小化（あるいは最大化）する可能解は、最適解と呼ばれる。

数学においてよくある最適化問題は、最小化に関するものである。最小化問題においては，「可能領域が凸領域でかつ目的函数がそこに於ける凸関数」となっていない場合には，一般に複数の局所最小解が存在しうる。ここで　x^*　が局所最小解であるとは、ある定数 δ > 0 が存在して、

${\displaystyle \|\mathbf {x} -\mathbf {x} ^{*}\|\leq \delta ;\,}$

を満たすような任意の x に対して次が成立することをいう。

${\displaystyle f(\mathbf {x} ^{*})\leq f(\mathbf {x} ).}$

すなわち、点 x^* はその（十分小さな）近傍内での最小点である。局所最大解も同様に定義される。

対比して問題の可能領域A全体における最小点のことを大域（的な）最小点ということがある。

記号

最適化問題では、しばしば特殊な記号が用いられる。ここではそれらのいくつかを紹介する。

函数の最小値と最大値

次の記号を考える：

${\displaystyle \min _{x\in \mathbb {R} }\;(x^{2} 1).}$

これは x を実数の集合 ${\displaystyle \mathbb {R} }$ から選んだときの目的函数 ${\displaystyle x^{2} 1}$ の最小値を意味する。この場合の最小値は ${\displaystyle x=0}$ のときの ${\displaystyle 1}$ である。

同様に、記号

${\displaystyle \max _{x\in \mathbb {R} }\;2x}$

は、任意の実数 x に対する目的函数 2x の最大値を意味する。この場合、目的函数は非有界なのでそのような最大値は存在せず、「無限大」あるいは「定義されない」が答えとなる。

最適入力引数

次の記号を考える。

${\displaystyle {\underset {x\in (-\infty ,-1]}{\operatorname {arg\,min} }}\;(x^{2} 1).}$

あるいは、次の同値なものを考える。

${\displaystyle {\underset {x}{\operatorname {arg\,min} }}\;(x^{2} 1),\;{\text{subject to:}}\;x\in (-\infty ,-1].}$

これは、区間 ${\displaystyle (-\infty ,-1]}$ において目的函数 x²   1 を最小化する引数 x 自身の値を与える（その函数の最小値がどのような値であるかはここでは問題とされない）。この場合、x = 0 は不可能、すなわち実行可能領域に属さないため、答えは x = -1 となる。

同様に

${\displaystyle {\underset {x\in [-5,5],\;y\in \mathbb {R} }{\operatorname {arg\,max} }}\;x\cos(y)}$

あるいは

${\displaystyle {\underset {x,\;y}{\operatorname {arg\,max} }}\;x\cos(y),\;{\text{subject to:}}\;x\in [-5,5],\;y\in \mathbb {R} }$

は、x が区間 ${\displaystyle [-5,5]}$ に属するという制約の下で、目的函数 ${\displaystyle x\cos(y)}$ の値を最大化する ${\displaystyle (x,y)}$ のペアを意味する（再び、その関数の最大値については問われていない）。この場合の解は、すべての整数 k に対する (5, 2kπ) と (−5,(2k 1)π) である。

arg min と arg max はしばしば、argmin および argmax と書かれることもあり、それらは「最小値の引数」および「最大値の引数」を意味する。

歴史

フェルマーとラグランジュは解が最適であるための条件を微分積分学を利用して求めた。一方でニュートンとガウスは最適解に向かって収束させる反復法を提唱した。

ある種の最適化問題に関する線型計画法という語はジョージ・ダンツィクによるものである。一方で、1939年にレオニート・カントロヴィチによって多くの理論が構築された（この文脈における「計画法（programming）」はコンピュータ・プログラミングとは異なり、アメリカ軍隊によって訓練や物流のスケジュールを表すために用いられていた "program" （講演会などの"プログラム"と同様の意味）が語源である。ダンツィクは当時その研究をしていた）。ダンツィクは1947年に Simplex Algorithm（シンプレックス法）を出版し、ジョン・フォン・ノイマンは同年に双対性の理論を発展させた。

その他の主要な数理最適化の研究者を以下に挙げる：

脚注

関連項目