гғҲгғӯгғ”гӮ«гғ«е№ҫдҪ•еӯҰпјҲиӢұиӘһ: Tropical geometryпјүгҒҜеҚ—зұігҒ§гҒҜгҒҳгҒҫгҒЈгҒҹж–°гҒ—гҒ„жј”з®—иҰҸеүҮгҒ«й–ўгӮҸгӮӢе№ҫдҪ•еӯҰгҒ®гҒ“гҒЁгҒ§гҖҒе’ҢгӮ’жңҖе°ҸеҖӨй–ўж•°пјҲгҒҫгҒҹгҒҜжңҖеӨ§еҖӨй–ўж•°пјүгҖҒз©ҚгӮ’йҖҡеёёгҒ®е’ҢгҒ«еӨүжӣҙгҒ—гҒҹгӮӮгҒ®гҒ§гҒӮгӮӢгҖӮзү№гҒ«гӮўгғЎгғјгғҗгӮ„д»Јж•°е№ҫдҪ•еӯҰгӮ„и¶…йӣўж•ЈгҒЁгҒ®й–ўйҖЈгҒҢж·ұгҒ„гҖӮгғҲгғӯгғ”гӮ«гғ«гҒЁгҒ„гҒҶе‘јз§°гҒҜгҖҒгғ–гғ©гӮёгғ«дәәж•°еӯҰиҖ…гғ»иЁҲз®—ж©ҹ科еӯҰиҖ…гҒ®гӮӨгғ гғ¬гғ»гӮ·гғўгғігҒ«еӣ гӮҖгҖӮ
е®ҡзҫ©
гҒ«д»ҘдёӢгҒ®жј”з®—
гӮ’е…ҘгӮҢгӮӢгҒЁгҖҒвҲһгӮ’йӣ¶е…ғгҖҒ0гӮ’еҚҳдҪҚе…ғгҒЁгҒҷгӮӢеҸҜжҸӣгҒӘеҶӘзӯүеҚҠз’°гҒЁгҒӘгӮӢгҖӮ гӮ’гғҲгғӯгғ”гӮ«гғ«еҚҠз’°пјҲгҒӮгӮӢгҒ„гҒҜ min-plus д»Јж•°пјүгҒЁгҒ„гҒҶгҖӮпјҲ гҒ«жңҖеӨ§еҖӨй–ўж•°гҒ«гӮҲгӮӢе’ҢгҖҒйҖҡеёёгҒ®е’ҢгҒ«гӮҲгӮӢз©ҚгӮ’е…ҘгӮҢгҒҹгӮӮгҒ®гӮ’гғҲгғӯгғ”гӮ«гғ«еҚҠз’°гҒЁгҒ„гҒҶгҒ“гҒЁгӮӮгҒӮгӮӢгҖӮпјү
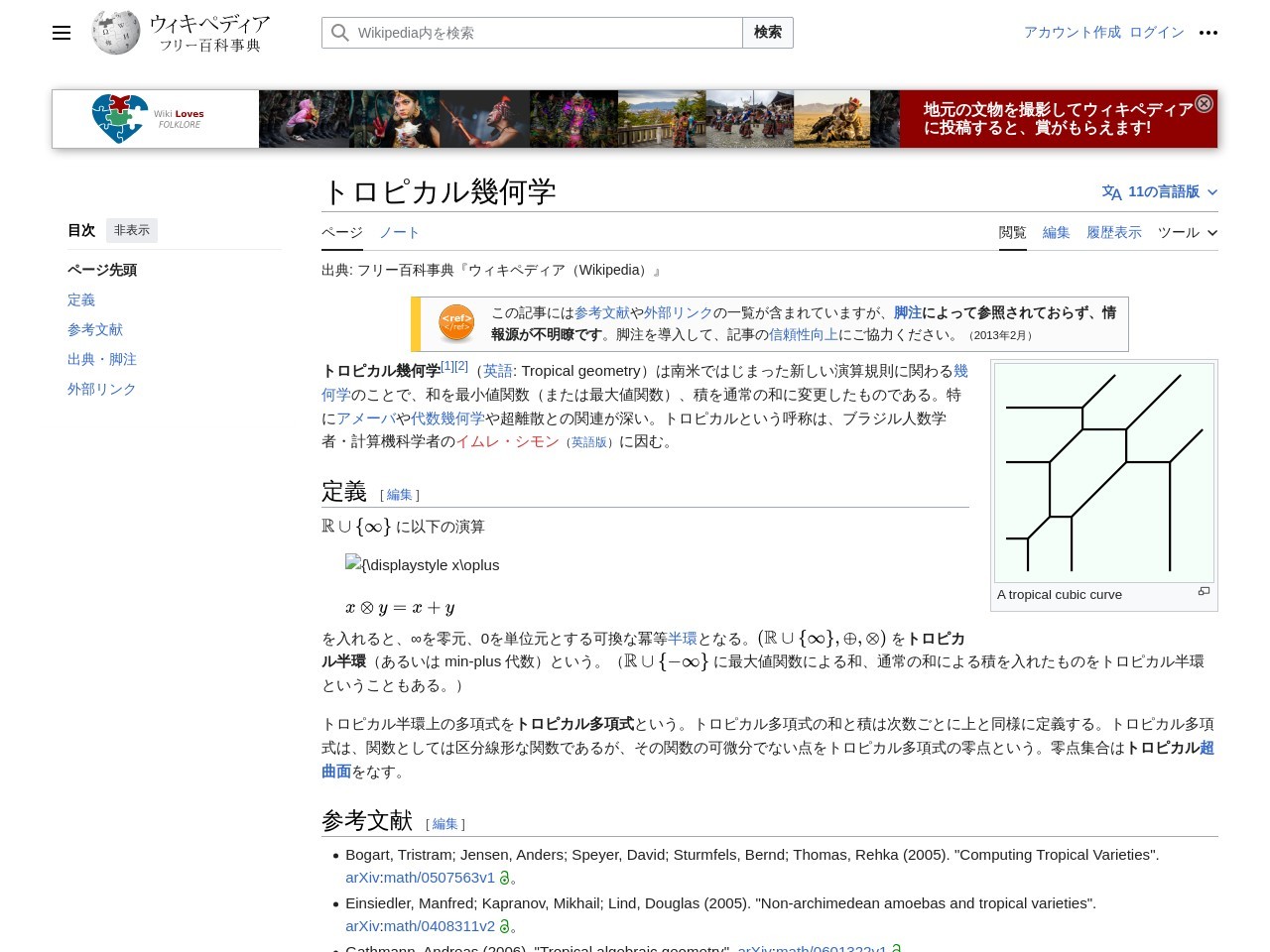
гғҲгғӯгғ”гӮ«гғ«еҚҠз’°дёҠгҒ®еӨҡй …ејҸгӮ’гғҲгғӯгғ”гӮ«гғ«еӨҡй …ејҸгҒЁгҒ„гҒҶгҖӮгғҲгғӯгғ”гӮ«гғ«еӨҡй …ејҸгҒ®е’ҢгҒЁз©ҚгҒҜж¬Ўж•°гҒ”гҒЁгҒ«дёҠгҒЁеҗҢж§ҳгҒ«е®ҡзҫ©гҒҷгӮӢгҖӮгғҲгғӯгғ”гӮ«гғ«еӨҡй …ејҸгҒҜгҖҒй–ўж•°гҒЁгҒ—гҒҰгҒҜеҢәеҲҶз·ҡеҪўгҒӘй–ўж•°гҒ§гҒӮгӮӢгҒҢгҖҒгҒқгҒ®й–ўж•°гҒ®еҸҜеҫ®еҲҶгҒ§гҒӘгҒ„зӮ№гӮ’гғҲгғӯгғ”гӮ«гғ«еӨҡй …ејҸгҒ®йӣ¶зӮ№гҒЁгҒ„гҒҶгҖӮйӣ¶зӮ№йӣҶеҗҲгҒҜгғҲгғӯгғ”гӮ«гғ«и¶…жӣІйқўгӮ’гҒӘгҒҷгҖӮ
еҸӮиҖғж–ҮзҢ®
еҮәе…ёгғ»и„ҡжіЁ
еӨ–йғЁгғӘгғігӮҜ
- Tropical Geometry, I

![]()