予測区間

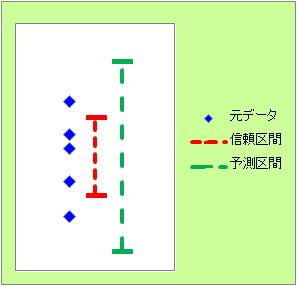
予測区間（よそくくかん）とは統計学用語で、母集団を仮定した上で、将来観察されるであろう標本値（現在は測定できない）に対して「どの範囲にあると予測されるか」を示すものである。

これに対し、信頼区間とは、母集団の母数（標本から測定できない）に対して 「どの範囲にあると推定できるか」を示すものである。混同しないように注意。

例

正規分布に従う母集団から標本を抽出したとしよう。母集団の平均と標準偏差は不明である（標本から推定できるのみ）。n を標本サイズ、 μと σ を母集団の平均と標準偏差とし、 X₁, ...,X_n を現在までの標本として、これから次の観察値X_{n 1} を予測したい。現在までの標本の平均および分散を

${\displaystyle {\overline {X}}_{n}=(X_{1} \cdots X_{n})/n}$

${\displaystyle S_{n}^{2}={1 \over n-1}\sum _{i=1}^{n}(X_{i}-{\overline {X}}_{n})^{2}}$

とする。ここで次の数値：

${\displaystyle {T_{n-1}}\sim {X_{n 1}-{\overline {X}}_{n} \over {\sqrt {S_{n}^{2} S_{n}^{2}/n}}}={X_{n 1}-{\overline {X}}_{n} \over S_{n}{\sqrt {1 1/n}}}}$

を考えると、これはスチューデントのt分布（自由度 n − 1 ）に従うことが示される。従って

${\displaystyle \Pr \left({\overline {X}}_{n}-T_{a}S_{n}{\sqrt {1 (1/n)}}\leq X_{n 1}\leq {\overline {X}}_{n} T_{a}S_{n}{\sqrt {1 (1/n)}}\,\right)=p}$

とすれば、T_a は自由度 n − 1 のt分布における 100((1 p)/2)パーセント点である。そして

${\displaystyle {\overline {X}}_{n}\pm T_{a}{S}_{n}{\sqrt {1 (1/n)}}}$

という数値が X_{n 1} に対する100p%予測区間の境界を表す。

例えば p = 0.95 とすれば、95%予測区間ということになる。

関連項目

• 傾向推定