リーマン関数

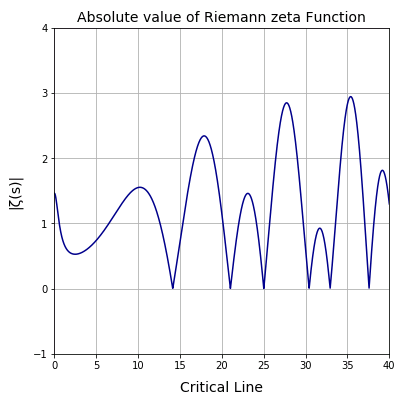
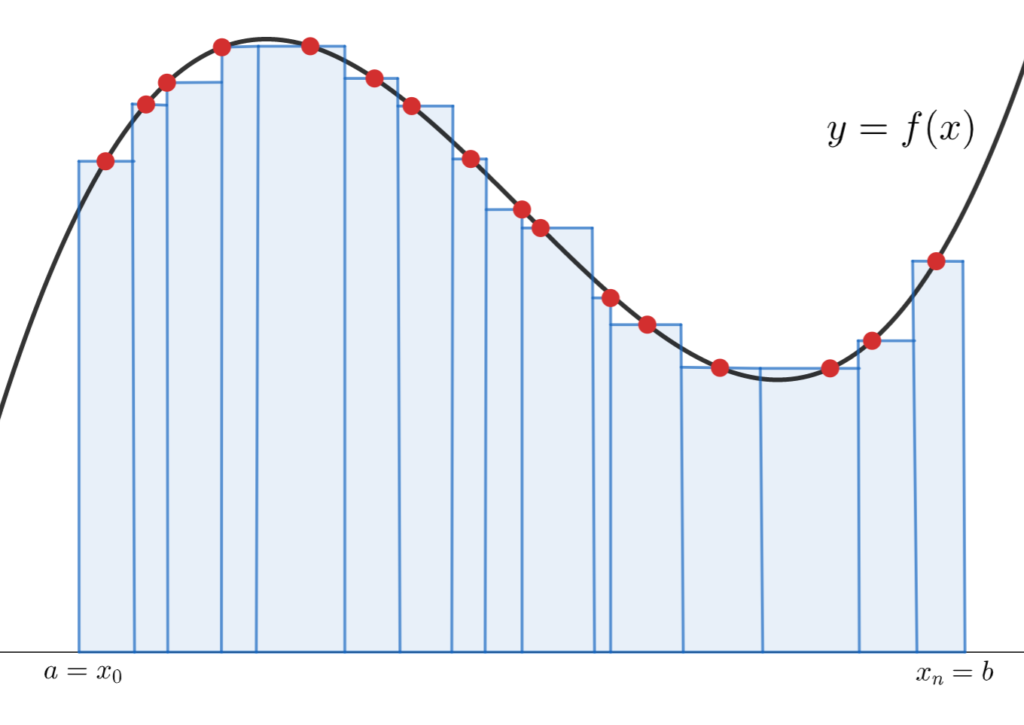
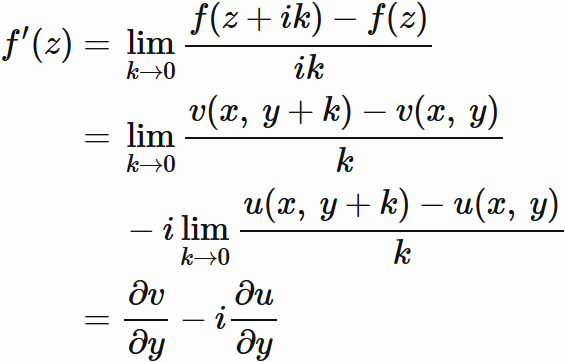リーマン関数 (英: Riemann function) は、1861年にリーマンが「至るところ微分不可能な連続関数」の例として使用したとされる次の関数である。

${\displaystyle f(x)=\sum _{n=1}^{\infty }{\frac {\sin {(n^{2}x)}}{n^{2}}}}$

しかしながら、次の条件で微分可能であることがわかっている。

${\displaystyle f'(x_{0})=-{\frac {1}{2}}}$

ここで、${\displaystyle x_{0}=\pi {\frac {2A 1}{2B 1}}\quad A,B\in \mathbb {Z} }$

参考文献

• Weisstein, Eric W. "Weierstrass function". mathworld.wolfram.com (英語).（内容はリーマン関数のもの）
• THE DIFFERENTIABILITY OF THE RIEMANN FUNCTION AT CERTAIN RATIONAL MULTIPLES OF π, JOSEPH GERVER, COLUMBIA COLLEGE, COLUMBIA UNIVERSITY, 1969.
• J. Gerver, The differentiability of the Riemann function at certain rational multiples of π, Amer. J. Math. 92 (1970), 35--55.  
• J. Gerver, More on the differentiability of the Riemann function, ibid 93 (1971), 33-41.

外部リンク

• Continuous Nowhere Differentiable Functions, Johan Thim, Department of Mathematics, Lulea University of Technology, 2003.(修士論文)

関連項目

• ワイエルシュトラス関数
• 病的な関数