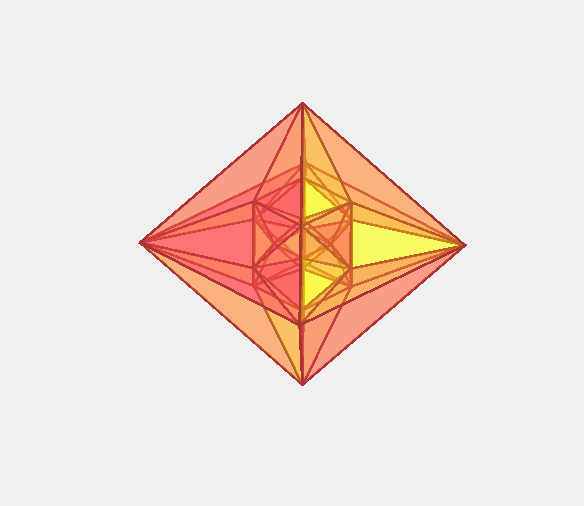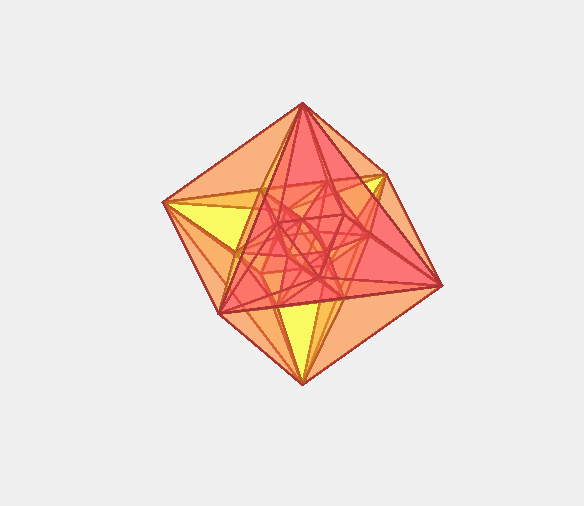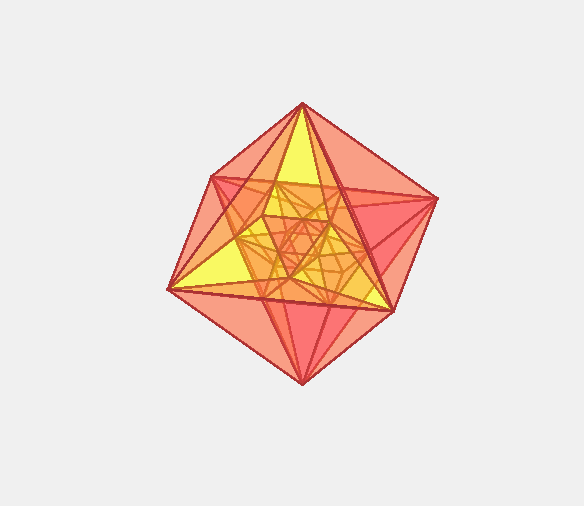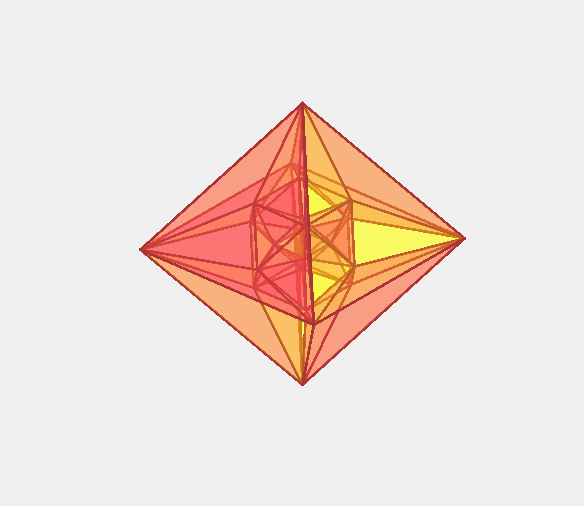
жӯЈеҚҒе…ӯиғһдҪ“пјҲгҒӣгҒ„гҒҳгӮ…гҒҶгӮҚгҒҸгҒ»гҒҶгҒҹгҒ„пјҢRegular hexadecachoronпјүгҒЁгҒҜгҖҒ еӣӣж¬Ўе…ғжӯЈеӨҡиғһдҪ“гҒ®дёҖзЁ®гҒ§16еҖӢгҒ®жӯЈеӣӣйқўдҪ“гҒӢгӮүгҒӘгӮӢгҖҒеӣӣж¬Ўе…ғгҒ®жӯЈи»ёдҪ“гҒ§гҒӮгӮӢгҖӮеҚҳзӢ¬гҒ§з©әй–“е……еЎ«гҒҢеҸҜиғҪгҒ§гҒӮгӮӢгҖӮ
- иғһпјҲж§ӢжҲҗз«ӢдҪ“пјүпјҡжӯЈеӣӣйқўдҪ“16еҖӢ
- йқўпјҡ32жһҡгҒ®еҗ„жӯЈдёүи§’еҪўгҒ«жӯЈеӣӣйқўдҪ“2еҖӢгҒҢйӣҶгҒҫгӮӢгҖӮ
- иҫәпјҡ24жң¬гҒ®еҗ„иҫәгҒ«жӯЈдёүи§’еҪў4жһҡгҖҒжӯЈеӣӣйқўдҪ“4еҖӢгҒҢйӣҶгҒҫгӮӢгҖӮ
- й ӮзӮ№пјҡ8еҖӢгҒ®еҗ„й ӮзӮ№гҒ«иҫә6жң¬гҖҒжӯЈдёүи§’еҪў12жһҡгҖҒжӯЈеӣӣйқўдҪ“8еҖӢгҒҢйӣҶгҒҫгӮӢгҖӮгҒқгҒ®еә§жЁҷгҒҜ (Вұ1, 0, 0,0)пјҲиӨҮеҸ·д»»ж„ҸпјүгҒ®е…ЁгҒҰгҒ®зҪ®жҸӣгҒ§гҒӮгӮӢгҖӮ
- еҸҢеҜҫпјҡжӯЈе…«иғһдҪ“
- гӮ·гғҘгғ¬гғјгғ•гғӘиЁҳеҸ·пјҡ{3,3,4}
иғһгҖҒйқўгҖҒиҫәгҖҒй ӮзӮ№гҒ®ж•°гҒҜгғ‘гӮ№гӮ«гғ«гҒ®гғ”гғ©гғҹгғғгғүгҒ®з¬¬5ж®ө(Layer 4)гҒ®дёүи§’еҪўгҒ®еҗ„ж®өгҒ®ж•°еӯ—гҒ®з·Ҹе’ҢгҒ«зӯүгҒ—гҒ„гҖӮеҸҚеҜҫеҒҙгҒ«гҒӮгӮӢиғһгҒ®дёӯеҝғеҗҢеЈ«гӮ’зөҗгҒ¶з·ҡгҒ«жІҝгҒЈгҒҰиҰӢгҒҹе ҙеҗҲгҖҒиғһгҖҒйқўгҖҒиҫәгҖҒй ӮзӮ№гҒҜеҗ„ж®өгҒ®ж•°еӯ—йҖҡгӮҠгҒ®гӮ°гғ«гғјгғ—гҒ«еҲҶеүІгҒ•гӮҢгӮӢгҖӮгҒҫгҒҹйқўгҖҒиҫәгҖҒй ӮзӮ№гҒ«йӣҶгҒҫгӮӢеӣіеҪўгҒ®ж•°гҒҜгҒқгӮҢгҒһгӮҢ第2ж®ө(Layer 1)гҖҒ第3ж®ө(Layer 2)гҖҒ第4ж®ө(Layer 3)гҒ®дёүи§’еҪўгҒ®еҗ„ж®өгҒ®ж•°еӯ—гҒ®з·Ҹе’ҢгҒ«зӯүгҒ—гҒҸгҖҒгҒқгӮҢгҒһгӮҢз·ҡеҲҶгҒ®з«ҜзӮ№гҒ®ж•°гҖҒжӯЈж–№еҪўгҒ®й ӮзӮ№гҒЁиҫәгҒ®ж•°гҖҒжӯЈе…«йқўдҪ“гҒ®й ӮзӮ№гҒЁиҫәгҒЁйқўгҒ®ж•°гҒ«зӯүгҒ—гҒ„гҖӮ
и„ҡжіЁ