クネーザーの定理 (微分方程式)

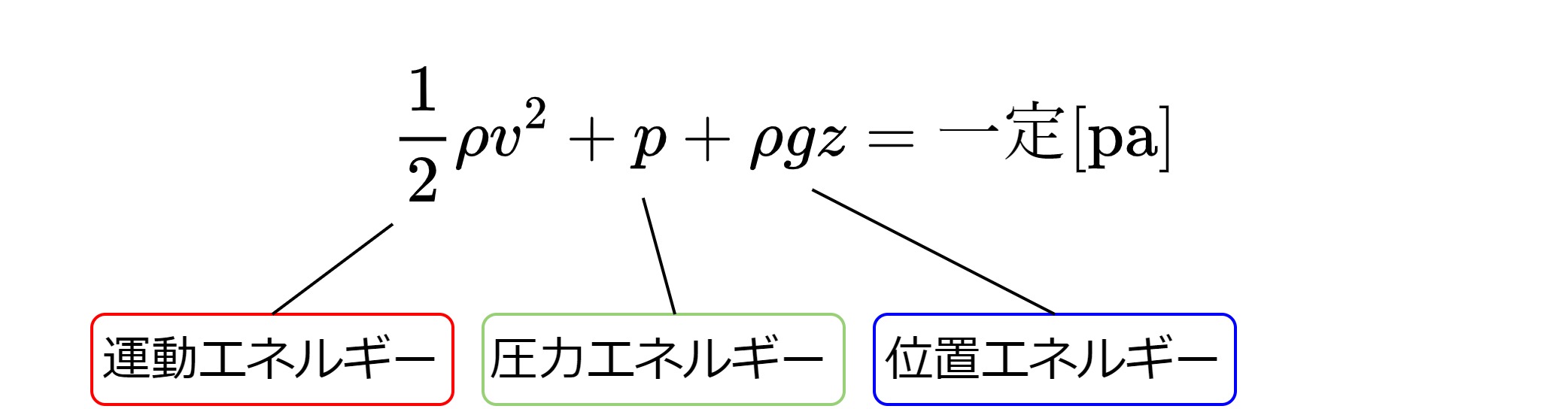
数学の常微分方程式の分野におけるクネーザーの定理（クネーザーのていり、英: Kneser's theorem）とは、微分方程式が振動的であるかどうかを決定付ける基準について述べた定理である。アドルフ・クネーザーの名にちなむ。

定理の内容

次の形状の線型同次常微分方程式を考える。

${\displaystyle y'' q(x)y=0.\,}$

ただし

${\displaystyle q:[0, \infty )\to \mathbb {R} }$

は連続関数である。この方程式は、無限個の零点を伴う解 y を持つとき振動的（oscillating）と言われ、そうでない場合は非振動的（non-oscillating）と言われる。

クネーザーの定理では、この方程式が非振動的であるための十分条件は

${\displaystyle \limsup _{x\to \infty }x^{2}q(x)<{\tfrac {1}{4}}}$

であり、振動的であるための十分条件は

${\displaystyle \liminf _{x\to \infty }x^{2}q(x)>{\tfrac {1}{4}}}$

であることが述べられている。

例

クネーザーの定理の内容を確かめるための例として、

${\displaystyle q(x)=\left({\frac {1}{4}}-a\right)x^{-2}\quad {\text{for}}\quad x>0}$

である場合を考える。ただし ${\displaystyle a}$ はゼロでない実数とする。今、

${\displaystyle \limsup _{x\to \infty }x^{2}q(x)=\liminf _{x\to \infty }x^{2}q(x)={\frac {1}{4}}-a}$

が成立するため、定理にしたがうと、解が振動的か非振動的かという点は、${\displaystyle a}$ が正である（非振動的）か負である（振動的）かという点に依存することが分かる。

この ${\displaystyle q(x)}$ の選び方に対する解を見つけ、この例に対する定理の成立を確かめるために、

${\displaystyle y(x)=x^{n}\,}$

の形状の解を代入する。すると、

${\displaystyle n(n-1) {\frac {1}{4}}-a=\left(n-{\frac {1}{2}}\right)^{2}-a=0}$

が得られるが、これは（ゼロでない ${\displaystyle a}$ に対し）一般解が

${\displaystyle y(x)=Ax^{{\frac {1}{2}} {\sqrt {a}}} Bx^{{\frac {1}{2}}-{\sqrt {a}}}}$

で与えられることを意味する。ここで ${\displaystyle A}$ と ${\displaystyle B}$ は任意定数である。

正の ${\displaystyle a}$ に対して解が非振動的であることを確かめることは難しくない。一方、負の ${\displaystyle a=-\omega ^{2}}$ に対しては、等式

${\displaystyle x^{{\frac {1}{2}}\pm i\omega }={\sqrt {x}}\ e^{\pm (i\omega )\ln {x}}={\sqrt {x}}\ (\cos {(\omega \ln x)}\pm i\sin {(\omega \ln x)})}$

が成り立つことから、解が振動的であることが確かめられる。

この例より、一般的な結果としてスツルム＝ピコーンの比較定理が成立する。

拡張

この結果には多くの拡張が存在する。近年の成果として、参考文献 を参照されたい。

参考文献