周期倍分岐

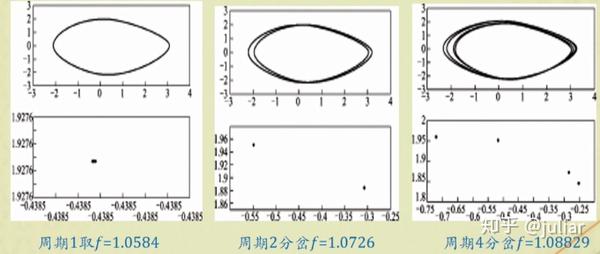
力学系において周期倍分岐（しゅうきばいぶんき、period-doubling bifurcation）とは分岐の一種である。

この分岐では、パラメータが変化していきある値に達すると、安定な不動点が不安定化し、その両側に安定な2周期点が発生する。

具体例

${\displaystyle x}$を実数、${\displaystyle \mu }$を実数のパラメータとして、1次元写像

${\displaystyle x\to f(x,\mu )=-x-\mu x x^{3}}$

を考える。

${\displaystyle x=0}$は${\displaystyle \mu <0}$においては安定な不動点である(${\displaystyle f(x,\mu )=x}$を満たす1周期点である)が、${\displaystyle \mu >0}$においては不安定であり、また${\displaystyle \mu >0}$において

${\displaystyle f({\sqrt {\mu }},\mu )=-{\sqrt {\mu }}}$

かつ

${\displaystyle f(-{\sqrt {\mu }},\mu )={\sqrt {\mu }}}$

であることから、${\displaystyle x=\pm {\sqrt {\mu }}}$は2周期点となっていて、かつ安定である。

従って、${\displaystyle \mu }$が負から正に増加していく過程で0を跨ぐ瞬間に、安定な不動点(1周期点)が不安定化し、その代わりに安定な2周期点がその両側に生じたことになる。

このことから、上記の1次元写像は${\displaystyle \mu =0}$を境に周期倍分岐を起こしたと言う。

関連項目

• 分岐図

参考文献

• 小室元政(2005)『新版 基礎からの力学系 分岐解析からカオス的遍歴へ』、サイエンス社