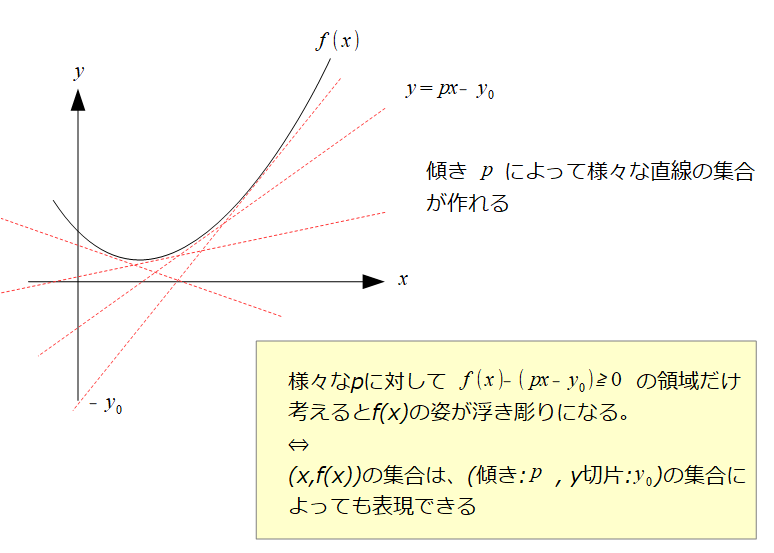
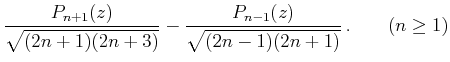ルジャンドル定数

ルジャンドル定数（ルジャンドルていすう、英語: Legendre's constant）は、アドリアン＝マリ・ルジャンドルにより素数計数関数${\displaystyle \pi (x)}$の漸近的振る舞いを捉えるために予想された式に含まれる数学定数である。現在、この値はぴったり1であることが分かっている。

ルジャンドルは、既知の素数に関して使用できた数値的証拠を研究し、${\displaystyle \pi (x)}$が近似式を満たしていることを考えた。

ルジャンドルが1808年にした予想は

${\displaystyle \pi (x)={\frac {x}{\ln(x)-B(x)}}}$

ここで${\displaystyle \lim _{x\to \infty }B(x)=1.08366}$....A228211 である。 もしくは同様にして

${\displaystyle \lim _{n\to \infty }\left(\ln(n)-{n \over \pi (n)}\right)=B}$

ここでBはルジャンドル定数である。ルジャンドルはBがおよそ1.08366であると推測したが、その正確な値にかかわらずBの存在は素数定理を暗に含む。

1849年にパフヌティ・チェビシェフがBに極限が存在するとき、Bは1に等しくなくてはならないことを証明した。より簡単な証明がPintzにより1980年に与えられている。

これは、誤差項の明示的推定を伴う正確な形式の下での、素数定理の直接的な帰結である。

${\displaystyle \pi (x)={\rm {Li}}(x) O\left(xe^{-a{\sqrt {\ln x}}}\right)\quad {\text{as }}x\to \infty }$

（ある正の定数aの場合。ここでO(…) はランダウの記号である）。これは1899年にCharles de La Vallée PoussinによってBが実際に1に等しいことが証明された。（素数定理は1896年にジャック・アダマールとLa Vallée Poussinにより独立に証明されたが、関連する誤差項の推定はなかった。）

このように単純な数値と評価されることで、ルジャンドル定数という用語はほぼ歴史的価値のある定数となった。（専門的には誤りであるが）しばしばルジャンドルが最初に推測した1.08366...という値が参照されることがある。

2010年にピエール・デザルトは次の式を証明した。

${\displaystyle {\frac {x}{\ln x-1}}<\pi (x)}$ for ${\displaystyle x\geq 5393}$および

${\displaystyle \pi (x)<{\frac {x}{\ln x-1.1}}}$ for ${\displaystyle x\geq 60184}$.

これは次の形式と同じである。

${\displaystyle \pi (x)={\frac {x}{\ln(x)-B(x)}}}$ with ${\displaystyle 1$.

出典

外部リンク

• Weisstein, Eric W. "Legendre's constant". mathworld.wolfram.com (英語).