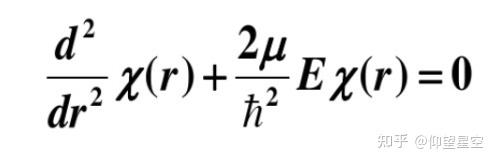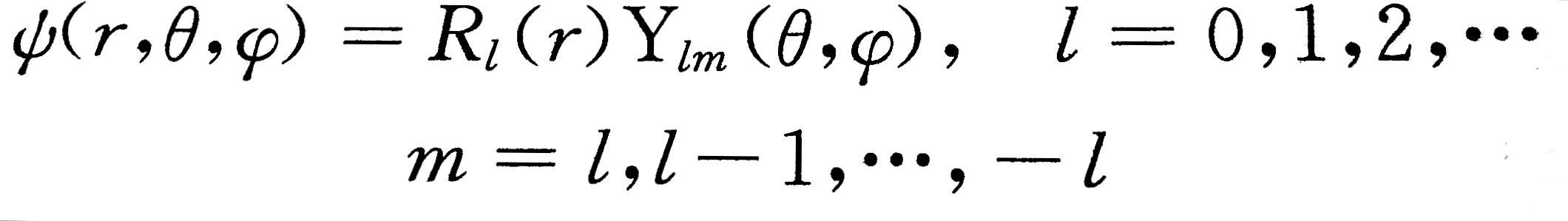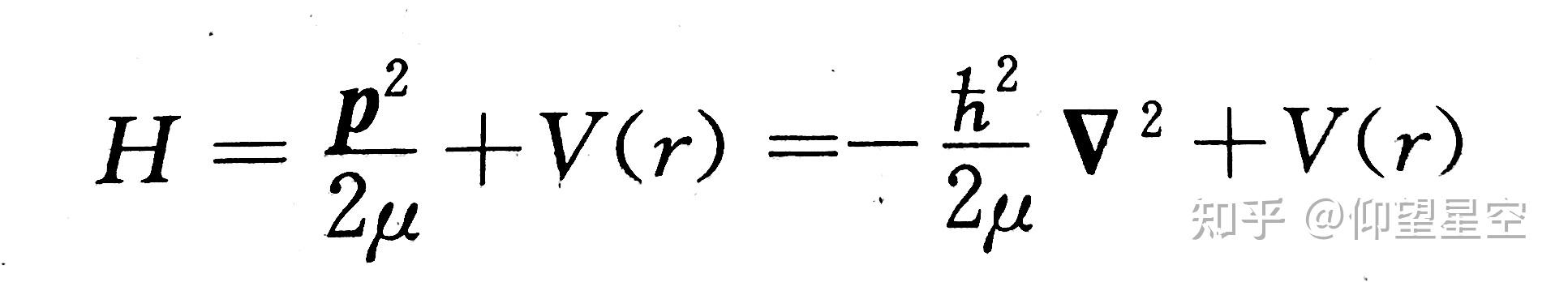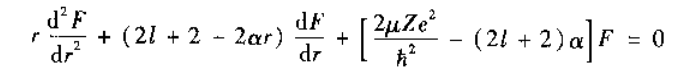中心力

中心力（ちゅうしんりょく、central force）は古典力学において、原点と物体を結ぶ線に沿っている方向に働く力である。

${\displaystyle {\boldsymbol {F}}({\boldsymbol {r}})=F({\boldsymbol {r}}){\hat {\boldsymbol {r}}}}$

ここで${\displaystyle {\boldsymbol {F}}}$は力、${\displaystyle {\boldsymbol {r}}}$は位置ベクトル、${\displaystyle |{\boldsymbol {r}}|}$はその長さ、${\displaystyle {\hat {\boldsymbol {r}}}={\boldsymbol {r}}/|{\boldsymbol {r}}|}$はその単位ベクトル、${\displaystyle F}$ はスカラー関数である。 中心力の議論では球対称性を仮定する場合も多く、その場合には${\displaystyle F({\boldsymbol {r}})}$は原点からの距離にのみ依存する量${\displaystyle F(|{\boldsymbol {r}}|)}$になる。 逆に球対称である場合には、力場は中心力場となる。

性質

中心力は保存場であるため、常にポテンシャルの負の勾配として表すことができる。

（積分の上限はポテンシャルが定義されている任意の定数である。）

保存場では、全力学的エネルギー（運動エネルギーとポテンシャルエネルギー）は保存される。

（ここで${\displaystyle {\dot {\boldsymbol {r}}}}$は${\displaystyle {\boldsymbol {r}}}$の時間微分を意味しており、言い換えれば速度である。）

また中心力場での角運動量は、力によるトルクがゼロであることより

である。結果として物体は角運動量ベクトルと垂直で原点を含む面を動き、ケプラーの第二法則に従う。（角運動量がゼロの場合、物体は原点と物体を結ぶ直線上を運動する。）

保存場であることの結果として、原点を例外として中心力場は渦なし（回転がゼロ）である。

例

重力とクーロン力は${\displaystyle F(r)}$が1/r²に比例する中心力の代表例である。このような負の${\displaystyle F}$（引力を意味する）の力場の物体は、ケプラーの法則に従う。

空間的調和振動子の力場は${\displaystyle F(r)}$が${\displaystyle r}$に比例し、符号が負である。

ベルトランの定理によれば、これら${\displaystyle F(r)=-k/r^{2}}$ と ${\displaystyle F(r)=-kr}$の場合は安定な閉じた軌道を持つ唯一の中心力場である。

ポテンシャル${\displaystyle V(r)}$が湯川ポテンシャルの場合も力は中心力となる。また重力の働く二質点間における二体問題は、その換算質量による中心力場での一体問題に帰着させることができる（他の中心力場でも同様に二体→一体に帰着できる）。

参考文献

関連項目

• 物理学
• 角運動量保存の法則
• 力学